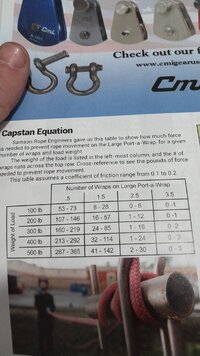
Bart said: "Still waiting for someone to calibrate a porty for tension ratio vs wraps. Its exponential."
I have developed my own rule of thumb for porta-wrap friction. Maybe it will be helpful to someone.
It obviously has to make many (too many) assumptions. But I still find it useful.
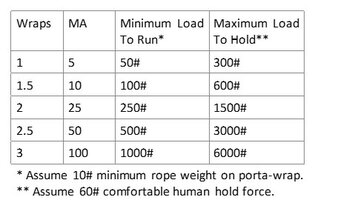
Here are my "rule of thumb" weight ranges for different wraps: [See PortaWrap Load Ranges. JPG]
View attachment 92166
This calls "One Wrap" when the rope comes in the porty at the top, goes under the porty once, then around the post on the top to the groundsman.
This assumes a Coefficient of Friction of 0.25 for nylon rope on aluminum porta-wrap. Ropes can vary a lot, higher and lower than this amount.
Reading the chart - If I estimate the load will be 125#, then 1.5 wraps might work, but groundsman would have to have a very light touch on the rope or the load won't run at all. For 125# 1 wrap would work much better, meaning it's easy to let run and easy to stop the load and hold it.
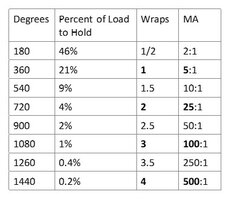
For those who want more precise measurements, here are the actual percentages, then how I fudged them to make them memorable.
View attachment 92167