Shadowscape
Been here a while
- Location
- far north
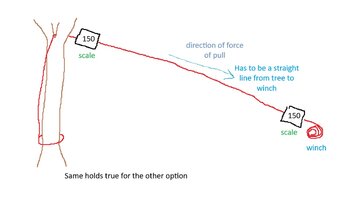
If the direction of pull was anything other than straight from the tree to the winch, the rope would have a big bow in it. That is just silly. You are letting this vector thing try and make up some new laws of physics that don't exist. There is a vector force, but it does not alter the direction of pull, nor does it alter the force of the pull.
@Muggs I'm not sure where you are going with pulleys on this problem. The fellow just wanted to know which was the easiest to pull with. Answer: They are equal. They both take the same force to pull the tree over, provided he cuts below his basal anchor. The direction of the pull must follow the rope. That is what you are pulling with!
