Steve Connally
Been here much more than a while
- Location
- Suffolk, Virginia
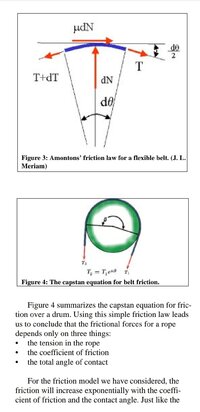
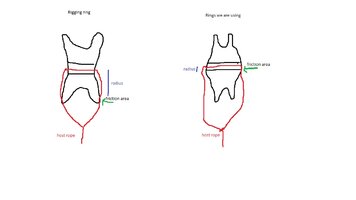
Wouldn't the friction on a larger bend radius equally add friction across a larger area, not change the location of the friction? Different way to ask this........Increasing bend radius puts more material in contact over a larger surface area changing the amount of friction across the bend......not changing where but adding more across the "where"? I get what you're saying but in terms of bend radius of rope across a surface there is no change to the location of where the friction is applied. Rite or am I missing something?