Mitch, you're getting sloppy with your terms and concepts. Dan's equation is the impact force equation. Google it. And it doesn't matter if the deceleration value is less than one: you aren't suddenly multiplying instead of dividing.
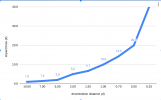
For simplicity, say the mgh term (potential energy) = 10 and d = 2, then F = 5. Now reduce d to 1 and F = 10. Now reduce d to 0.5 and F = 20. Now reduce d to 0.1 and F = 100. Which all makes sense, because the smaller the deceleration distance, the higher the force will be.
Speaking of force, the cut piece doesn't gain force during the fall; it gains velocity (at least until another force - aerodynamic drag, rises to the point of equalizing the force of gravity). The force acting on a horizontal limb that is suddenly freed from the tree by a chainsaw is gravity (otherwise it would hang there in free space) and the force of gravity isn't changing or increasing during the fall. What is increasing during the fall is the limb's velocity and momentum. What seems like an increase in force to you is the increase in deceleration force required by the groundie to remove the kinetic energy from the piece.
For simplicity, say the mgh term (potential energy) = 10 and d = 2, then F = 5. Now reduce d to 1 and F = 10. Now reduce d to 0.5 and F = 20. Now reduce d to 0.1 and F = 100. Which all makes sense, because the smaller the deceleration distance, the higher the force will be.
Speaking of force, the cut piece doesn't gain force during the fall; it gains velocity (at least until another force - aerodynamic drag, rises to the point of equalizing the force of gravity). The force acting on a horizontal limb that is suddenly freed from the tree by a chainsaw is gravity (otherwise it would hang there in free space) and the force of gravity isn't changing or increasing during the fall. What is increasing during the fall is the limb's velocity and momentum. What seems like an increase in force to you is the increase in deceleration force required by the groundie to remove the kinetic energy from the piece.