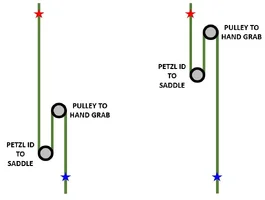
I should clarify what I said above, in that there is a difference where the pull comes from, whether from load itself (the climber) or from, say, the groundie, with my statement that the pull to raise your weight must equal your weight with a fixed upper pulley. This is not completely true If you yourself are the load, pulling on the tail of a DRT system or single upper pulley. It is more accurate to say that the pull must equal your weight only at the instant you are pulling. And by being the load yourself, you instantly reduce this by slightly more than half as soon as you lean hard into the pull. You transfer slightly more than half your weight off the load and onto the pull and so you rise. This feels like MA and indeed works to your advantage as such, but the actual ratio is in fact still technically 1:1, loaded weight at that instant vs. pull required at the same instant. You pull down with some weight which you automatically have instantly removed from the load side. On a practical level, I would have to agree this is a bastard form of mechanical advantage which feels to the climber as roughly 2:1 and this is what counts at that moment. So I admit I am not sure how useful all this technical discussion actually is to most of us. But I used to teach this stuff to shipyard riggers once upon a time, so it is easy to lapse into that mode.