Muggs
Been here much more than a while
- Location
- Canuckistan
Continuing from another thread about the difference between basal vs. canopy anchored pull lines for dropping trees, here's another question:
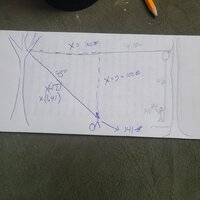
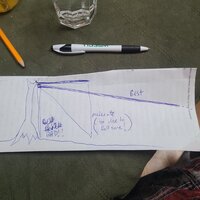
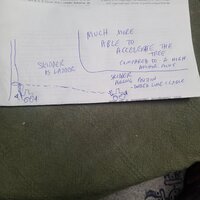
If I have a tree being felled and I want to pull it over using a rope tied directly to the trunk up top, assuming that I'm pulling on level ground, from a fixed distance, with a fixed input (ie winching) force, what does the math say about what height I should tie the rope? Assuming that the rope is acting only in the x axis (lateral direction) and y axis (vertical direction), with no sideways deflection (z axis), there must be a point of height where the pull begins to act more to pull the tree down into the ground, and less to pull it sideways. That is to say, there must be a point where the x-axis vector of the pull line gets overtaken by the y-axis vector. So let's say that I've determined that I can anchor the rope at any height, from 0 to 20m (65 ft) up without worrying about breaking the tree with my pull, where is the optimal height to anchor the rope? Or am I just overthinking it entirely and the answer is just "as high as possible"? I assume the mathematical way to answer this is some combination of trig and calculus, neither of which I have engaged in since high school. Hoping someone much smarter than myself can help with the math on this.
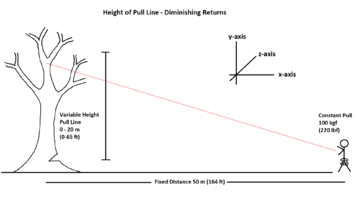
If I have a tree being felled and I want to pull it over using a rope tied directly to the trunk up top, assuming that I'm pulling on level ground, from a fixed distance, with a fixed input (ie winching) force, what does the math say about what height I should tie the rope? Assuming that the rope is acting only in the x axis (lateral direction) and y axis (vertical direction), with no sideways deflection (z axis), there must be a point of height where the pull begins to act more to pull the tree down into the ground, and less to pull it sideways. That is to say, there must be a point where the x-axis vector of the pull line gets overtaken by the y-axis vector. So let's say that I've determined that I can anchor the rope at any height, from 0 to 20m (65 ft) up without worrying about breaking the tree with my pull, where is the optimal height to anchor the rope? Or am I just overthinking it entirely and the answer is just "as high as possible"? I assume the mathematical way to answer this is some combination of trig and calculus, neither of which I have engaged in since high school. Hoping someone much smarter than myself can help with the math on this.

Last edited: